Reading Report – Management of Disasters #7

Book Name:

Part 3 / Implementation of systems analysis to management of disasters: Chapter 7 / Multi-objective analysis

Summary

The multifunctional nature and political hierarchy in emergency management organizations are well suited for hierarchical planning and multi-attribute multi-objective approaches, as various groups have different priorities before, during, and after a disaster hits. Multiple objective decisions concerning disaster management do not have an optimal solution. There have been great efforts to develop a methodology for assessing trade-offs between alternatives based on using more than one objective. a multiobjective programming problem is characterized by an r-dimensional vector of objective functions:

Z(x) = Z1(x), Z2(x), Z3(x), . . . , Zr (x) subject to x ∈ X where X is a feasible region:

X = {x : x ∈ Rn, gi (x) ≤ 0, x j ≥ 0 ∀ i, j}where R is the set of real numbers, gi(x) is the set of constraints, and x is the set of decision variables. The first step of the multiobjective analysis consists of identifying the set of nondominated solutions within the feasible region X. So instead of seeking a single optimal solution, a set of noninferior solutions is sought. The essential difficult with multiobjective analysis is that the meaning of the optimum is not defined as long as we deal with multiple objectives that are truly different. The focus of multiobjective analysis in practice is to sort out the mass of clearly dominated solutions, rather than determine the single best design. The result is the identification of a small subset of feasible solutions that are worthy of further consideration. Formally, this result is known as the set of nondominated solutions. In a multiobjective problem, any set of inputs, x, define a multidimensional space of feasible solutions, as Figure 7.1 indicates.

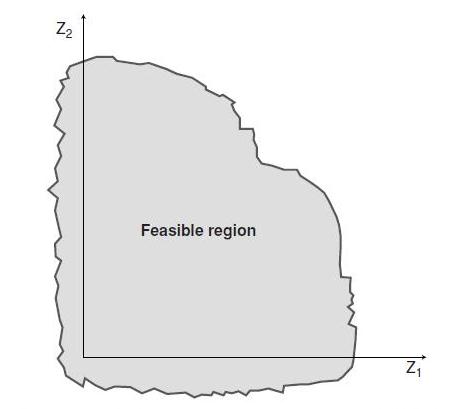
Figure 7.1 Feasible region of a multiobjective problem presented in the objective space.

The main characteristic of the nondominated set of solutions is that for each solution outside the set, there is a nondominated solution for which all objective functions are unchanged or improved and at least one is strictly improved. The preferred solution for any problem should be one of the nondominated solutions. If we introduce levels of acceptability for each of the objectives, the nondominated solutions are best divided into two categories: the major alternatives and the compromises. A major alternative group of nondominated solutions represents the best performance on some major objective. As Figure 7.2 indicates, the major alternatives represent polar extremes. A compromise group lies somewhere in between the major alternatives.

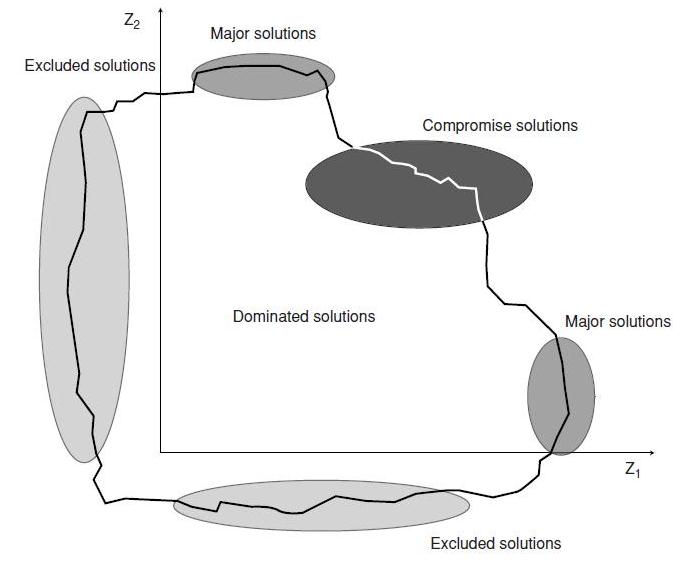
Figure 7.2 Classification of feasible multiobjective alternative solutions.

The remainder of the feasible region of solutions is likewise usefully categorized into dominated and excluded solutions. Dominated solutions are those that are inferior in all essential aspects to the other solutions. Excluded solutions are those that perform so badly on one or more objectives that they lie beneath the threshold of acceptability. Thus, they may be dropped from further consideration. Given a set of feasible solutions X, the set of nondominated solutions is denoted as S and define as follows:

S = {x : x ∈ X, there exists no other x’∈ X such that Zq (x_) > Zq (x) for some q{1, 2, . . . , r} and       Zk (x_)  Zk (x) for all k  q}

Multiobjective techniques are classified into three groups.

1. Methods for generating the nondominated set: This method considers a vector of objective functions then generate the subset of nondominated solutions in the initial feasible region and uses this vector to identify and deal strictly with the physical realities of the problem. The desired outcome is the identification of the set of nondominated solutions to help the decision maker gain insight into the physical realities of the problem at hand. There are several methods available to generate the set of nondominated solutions. These 4 methods , which are widely used, are weighting method, constraint method, Phillip’s linear multiobjective method and Zeleny’s linear multiobjective method. The first two methods transform the multiobjective problem into a single-objective programming format and by parametric variation of the parameters used to effect the transformation, the set of nondominated solutions can be generated. The weighting and constraint methods can be used to obtain nondominated solutions when the objective functions and constraints are nonlinear. The last two methods generate the nondominated set for linear models only. However, these two approaches do not require the transformation of the problem into a single-objective programming format.
2. Methods with prior articulation of preferences: Methods in this class are further divided into continuous and discrete methods.- Continuous Once the set of nondominated solutions for a multiobjective problem has been identified using any of the methods mentioned in the first group, the decision maker is able to select one of those nondominated solutions as her or his final choice. The best-known methods in the group of continuous methods with prior articulation of  references are goal programming, utility function assessment, and the surrogate worth trade-off method.- Discrete used when there are many decision situations in which the decision maker must choose among a finite number of alternatives that are evaluated on a common set of noncommensurable multiple objectives or criteria.
3. Methods with progressive articulation of preferences: The characteristic of the methods in this group are that a nondominated solution is identified and that the decision maker is solicited for trade-off information concerning this solution, and the problem is modified accordingly. There are so many methods that used to solve the problem but the author only introduced us two multiobjective analysis methods which are the weighting method and the compromise programming.

The weighting method belongs to the group of techniques for generating a nondominated set. It is based on the idea of assigning weights to the various objective functions, combining these into a single-objective function, and parametrically varying the weights to generate the nondominated set. Mathematically, the weighting method can be stated as follows:

Max Z(x) = w1 Z1(x) + w2 Z2(x)+· · ·+wr Zr (x) subject to x ∈ X

                      which can be thought of as an operational form of the formulation:

Max- dominate Z(x) = [Z1(x), Z2(x), . . . , Zr (x)] subject to x ∈ X

A multiobjective problem has been transformed through Equation into a single-objective optimization problem for which solution methods exist. The coefficient wi operating on the ith objective function, Zi(x), is called a weight and can be interpreted as the relative weight or worth of that objective compared with the other objectives. If the weights of the various objectives are interpreted as representing the relative preferences of some decision maker, then the solution to Equation is equivalent to the best compromise solution which is the optimal solution relative to a particular preference structure. The optimal solution to Equation is a nondominated solution, provided all the weights are positive. Therefore, the most that should be expected from the weighting method is an approximation of the nondominated set.

Compromise programming was originally developed as an interactive method with progressive articulation of decision-maker preferences. Compromise programming identified solutions that are closest to the ideal solution, as determined by some measure of distance. Due to its simplicity, transparency, and easy adaptation to both continuous and discrete settings, compromise programming is recommended as the multiobjective analysis method of choice for application to disaster management. From figure 7.3we can see that the solution for which both objectives (Z1, Z2) are maximized is point I (Z1 , Z2 ), where Z1 is the solution obtained by maximizing the objective i. It is clear that the solution I (named ideal point) belongs to the set of infeasible solutions. Let us consider a discrete case with four solutions available as a nondominated set {A, B, C, and D}. The solutions identifie as being closest to the ideal point are called compromise solutions, and constitute the compromise set. If we use a geometric distance, the set of compromise solutions may include a subset {A and B} of the nondominated set {A, B, C, and D}. The implementation of compromise programming results in a reduction of the nondominated set. If the compromise set is small enough to allow the decision maker to choose a satisfactory solution, then the algorithm stops. If not, the decision maker is asked to redefin the ideal point and the process is repeated.

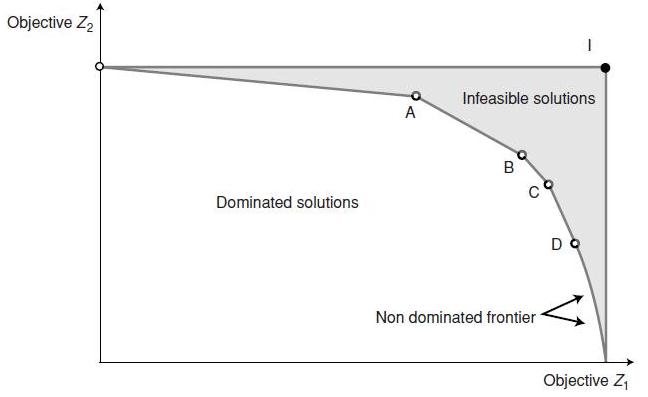
Figure 7.8 Illustration of compromise solutions.

Reporter’s Own Thoughts

Even though the multiobjective decision is not a tool that created for analyzing disaster management problem but it is still an appropriate tools to analyse some problems related in the field such as floodplan management problem. Since every disaster happened under different constraints, it is necessary to look at as many solution as we can to choose the best solution which is fit for the situation.