
平成19年1月22日 更新
はじめに
都市域における熱・水・物質の輸送過程には建物によって生み出された乱流構造が重要な役割を持ちます。本研究室では自然条件下での乱流構造を明らかにするべく、屋外スケールモデル(COSMO)で乱流構造の研究を行っています。

 |
都市キャノピー上に発達する乱流構造のスケールや形状といった特徴は未だ明らかになっておらず、透過性を有する植生キャノピー乱流との類似性が指摘される一方で、平板乱流の特徴を有することも指摘されています。
本研究では乱流組織構造の時空間スケールを抽出する新しい画像解析による構造抽出法OSIM(Organized Structure Identification Method)を提案しました。この手法では乱流構造を一つ一つ抽出することにより、個々の構造の持つ形状やスケール情報を残したままでの解析を行うことができます。
COSMOにおける乱流構造可視化
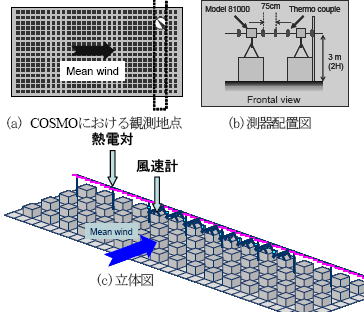
日本工業大学(埼玉県南埼玉郡宮代町)の敷地内に100 m × 50 mのコンクリート基盤を設け、その上に建物に見立てた一辺1.5 m (=H)のコンクリート立方体を規則的に512個(32個×16個)を建蔽率0.25で配列しています。
COSMO上における冬季の卓越風向に対し、熱電対を0.75m間隔で水平方向に60点配置しました。計測高度は3m(=2H)です。
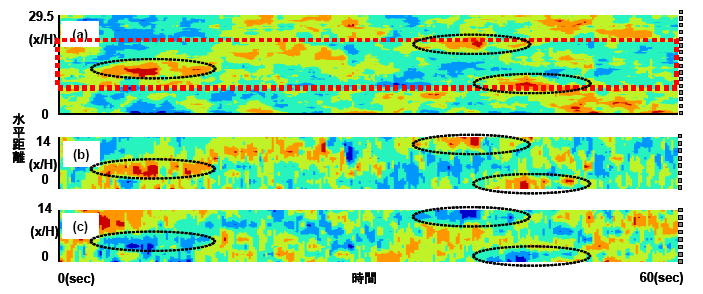
解析結果一例
図(a)に熱電対による一分間の温度変動値、図(b)に風速計による温度変動、図(c)に風速計による水平速度変動値を示します。それぞれ筋状の乱流構造が確認でき、風速計による温度変動と熱電対による温度変動はよく対応しています。また正の温度変動は低速領域、負の温度変動は高速領域に対応しているようです。
乱流構造抽出手法OSIMのアルゴリズム
上で示したコンター図による可視化結果をより定量的に把握するための「OSIM(乱流構造抽出法)」のアルゴリズムについて紹介します。時空間的に連続した温度変動を持つ領域を構造として認識し、各々の構造における水平方向の代表幅及び時間方向の代表持続時間を算出します。このアルゴリズムは大きく分けて下図のような三つで構成されます。
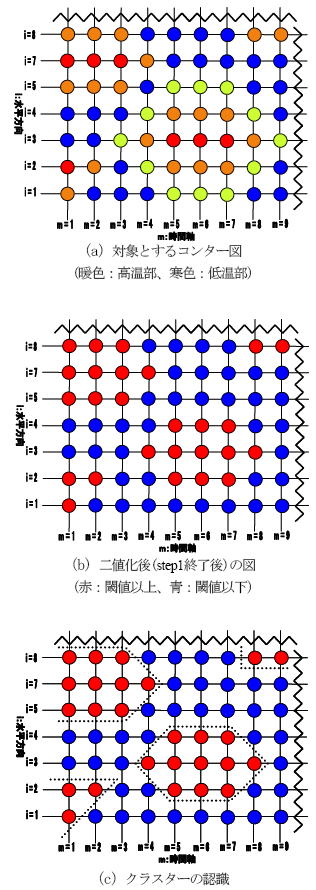
| ステップ1. 〜閾値による構造の選別〜 まず、水平・時間座標上の時間平均値からの温度変動値 を算出する。模式図(右図)は時間座標m=1〜9、水平座 標i=1〜8の領域を示しており、図(a)は各座標のもつ温度 変動値を色分けしたものである。青〜黄緑〜オレンジ〜 赤の順で変動値が大きくなるとする。 今、オレンジ及び赤が閾値を越えている点であり、青及 び黄緑は閾値を越えていない点とし、両者を識別する (図(b)参照)。 ステップ2. 〜クラスター化〜 閾値以上の点が座標上で縦・横・斜め方向に連続して いた場合、それらの点の集合を一つの構造と考える。 ステップ3. 〜個々の構造の特性把握〜 最後に、個々の構造の特性を決定する。例えば、各々 のクラスターに識別番号nを振り、それぞれの識別番号 ごとに1点刻みにスパン方向の最大座標と最小座標を求 め、その差を取り、それらの平均を求め、「構造nの代 表幅」とした。そして時間方向には各々の構造の持つ最 大時間座標と最小時間座標から差を求め、「構造nの代 表持続時間」とした。そして各々の構造に対し、代表幅 と代表持続時間の積を「構造nの水平・時間領域」と定 義し、それに温度変動の二乗を更に掛け合わせたものを 「構造nのエネルギー」と定義した。また、代表幅ごとに 構造を区分けし、区分け毎に「構造nのエネルギー」の 全観測データでの積算値を「エネルギー分布関数」と定 義する。 |
 |
適用例
一分間の温度変動を対象にこの構造抽出アルゴリズムを用いた例を示します。
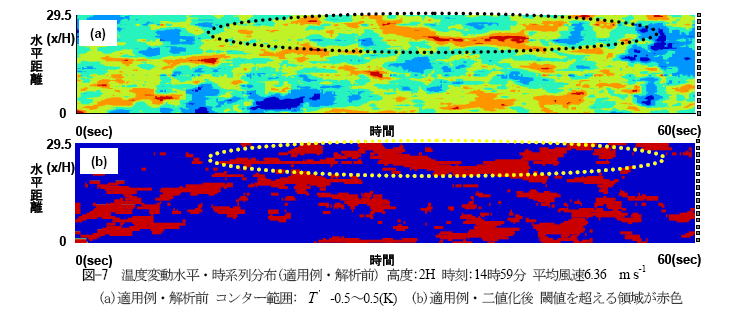
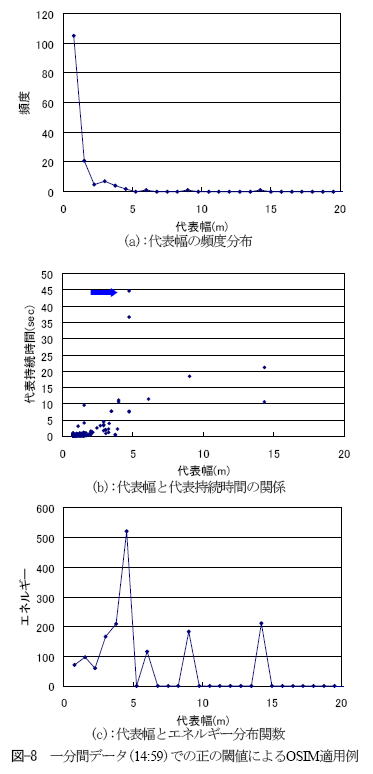
| 図-7(b)はステップ1の作業を終えたあとの出力結果です。 閾値を超えた領域が赤色で描かれています。 図-8(a)-(c)はOSIMによって得られた構造のスケール の統計解析の結果です。図-8(a)はこの一分間での各 構造の持つ代表幅の頻度分布であり、図-8(b)は各構造 の代表幅及び代表持続時間の関係を示しています。 図-8(b)の青矢印で示した点は代表持続時間が44.7sec (447点分)、代表幅が約4.5m(6点分)の構造を示していま すが、これは図-7(a)黒枠の構造に対応しています。また、 この青矢印で示したような構造は各代表幅に対し、長い 代表持続時間を持ちます。これらの点は低速ストリークと いった組織構造に対応しているものと思われます。 図-8(c)は代表幅と温度変動のエネルギー分布関数です。 図-8(a)では代表幅の小さいものが非常に多くの頻度を持 っていましたが、エネルギー分布で見てみると非常に小さい ことがわかります(図-8(c))。 一方、エネルギー分布関数のピークは代表幅が4.5m(6点分) 、 9m(12 点分) 、14.25m(19点分)であり、場の大きな変動をもた らす代表的な構造と考えることができます。 |
 |
まとめ
OSIM(乱流構造抽出法)は乱流構造を個別に解析することができるため、幅や長さ(持続時間)のみならず、曲がり具合や左右の非対称性などについても定量的に把握することができると考えられる。今後この手法を用いて、COSMOで観測されたデータから、外部気象条件(安定度、風向、風速)や、地表面条件(幾何形状、建蔽率)と乱流構造のスケール・形状の関係等明らかにしていく予定です。