Dr.中野の（Shinさんのための？）講義at 1999.3.11 13:00

M.S.Daw and M.I.Baskes, Phys.Rev.B, vol.29 No.12, pp.6443-6453(1984)

における式（６）の導出

−高橋のメモから高橋がアレンジ（間違っていたら高橋の責任）−

　

変数の定義：

変位； … テンソル．i,jは各々x,y,zとみなしていい．

座標系は任意の方向に取ることができる．

… ある原子を原点においた時，

他の原子の変位テンソル．i,jは各々，x,y,z．

は各原子につけた番号．

は平衡状態における．

歪み；

但し，

この意味は（中野流では），は独立に９個とることができるが，実際には６個．アンチシンメトリックなはちょうど３つあるので，これを適当に決めていい．だったら０にしよう．

桃園のコメントでは，rotation成分．

高橋は，当初，であること同義と思っていたが，この関係は定義した時点で満たされるので，同義ではない（納冨の指摘があった．）．おそらく桃園のコメントのようにrotationに対して，不変という関係から出てくるのではないか？と思うのだが…物理的なイメージを掴む必要があるので，そのうちやっておく必要がある…いつできるか…

　

　

式の導出：

無限固体の全エネルギーは個の原子からなるとすると

ある原子１個あたりのエネルギーは

但し，はその原子から別の原子までの距離で，はその原子以外の全ての原子に対する合計を取る．

すると系の「平衡条件」は

である．ここでは歪みテンソル．i,jは各々x,y,zとみなしていい．座標系は任意の方向に取ることができる．

であるので，

　

　

が平衡条件と同義となる．これは，歪みテンソルの各成分で偏微分しているが，原子の位置で微分する形に持ち込みたい．そこで，上で決めた，変位と歪みの定義式を使う．歪みは全原子の変位で決まるから，上の式を原子の位置を経由したした微分の式にかえてしまう．

　

　

この式での項から料理する．

上の定義より，

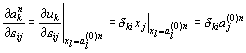
２つ目の等式の証明は証明１に示す．

次に，の項を料理すると，

さらに変形して

なので

なので

従って平衡条件は

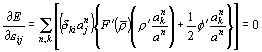
但し，平衡状態において，に注意．kに付いてのsummationはk=iの時以外，クロネッカーのデルタが0となるので，

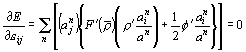
以上．

　

　

　

証明１：

上の式（　　）から，

両辺をで微分すると，

最後の等式に注目，

より

従って，

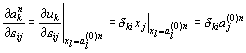
証明終わり．